Inhaltsverzeichnis
- FEM-Simulation
-
Wie funktioniert die FEM-Simulation?
- Was ist die Finite-Elemente-Methode?
- Welche mathematischen Grundlagen liegen der FEM zugrunde?
- Wie wird die Verformung und Belastung eines Bauteils berechnet?
- Ihr Ansprechpartner
FEM-Simulation
Die Finite-Elemente-Methode (FEM) hat sich als eine der führenden Technologien zur Berechnung und Simulation physikalischer Systeme etabliert. In der modernen Industrie ermöglicht die FEM-Simulation die präzise Analyse und Vorhersage von Verformungen, Spannungen und anderen physikalischen Größen in komplexen Bauteilen. Diese umfassende Methode wird in zahlreichen Branchen, u.a. in der Stahlindustrie bei der Entwicklung wassergekühlter Anlagensysteme und Apparate, angewendet und bietet Unternehmen wie der KSK GmbH in Haltern am See entscheidende Vorteile.
Wie funktioniert die FEM-Simulation?
Was ist die Finite-Elemente-Methode?
Die Finite-Elemente-Methode ist ein numerisches Verfahren zur Lösung von Differentialgleichungen, die physikalische Phänomene beschreiben. Sie basiert auf der Diskretisierung von Geometrien in eine Vielzahl von kleineren, einfacheren Elementen, wie Dreiecke oder Vierecke. Diese Elemente werden verwendet, um ein Gleichungssystem zu erstellen, das die physikalischen Verhaltensweisen des gesamten Systems approximiert. Durch die Verwendung von Ansatzfunktionen, die bestimmte mathematische Bedingungen erfüllen müssen, kann die FEM die Verschiebungen, Spannungen und Verformungen eines Bauteils berechnen.
Welche mathematischen Grundlagen liegen der FEM zugrunde?
Die FEM basiert auf der Methode der gewichteten Residuen und dem Prinzip der virtuellen Arbeit. Diese mathematischen Ansätze ermöglichen es, die Differentialgleichungen, die das physikalische Verhalten eines Systems beschreiben, in ein algebraisches Gleichungssystem zu überführen. Durch die Lösung dieses Gleichungssystems können die physikalischen Größen, wie Spannung und Verschiebung, in den diskreten Elementen des Modells bestimmt werden. Die Feinheit der Unterteilung und die Dichte des Netzes sind entscheidend für die Genauigkeit der FEM-Simulation.
Wie wird die Verformung und Belastung eines Bauteils berechnet?
Die Berechnung der Verformung und Belastung eines Bauteils durch FEM erfolgt durch die Anwendung von Lasten und Randbedingungen auf das diskretisierte Modell. Die FEM-Simulation löst das resultierende Gleichungssystem unter Berücksichtigung der physikalischen Gesetze, um die resultierenden Spannungen und Verformungen zu bestimmen. Die Wahl der Randbedingungen ist hierbei entscheidend, da sie die physikalischen Grenzen des Systems definieren und die Genauigkeit der Simulation beeinflussen.
Ihr Ansprechpartner

Prof. Dr.-Ing. Andreas Wichtmann
Simulation und FEM
+49 (0) 2364 10539-0
wichtmann@kskgruppe.de
Welche Anwendungen hat die FEM in der Industrie?
Wie wird die FEM in der Stahlindustrie genutzt?
In der Stahlindustrie wird die FEM zur Optimierung und Analyse von Bauteilen verwendet, die hohen Belastungen ausgesetzt sind. Die Simulation ermöglicht es Ingenieuren, die Spannungsverteilung innerhalb von Stahlkonstruktionen zu untersuchen und potenzielle Schwachstellen zu identifizieren. Durch die FEM können Unternehmen wie die KSK GmbH in Haltern am See die Lebensdauer ihrer Produkte verlängern und die Sicherheit ihrer Strukturen gewährleisten.
Welche Rolle spielt die FEM in der Metallbau-Branche?
Die FEM ist ein unverzichtbares Werkzeug für Metallbauer, da sie die präzise Analyse und Optimierung von Metallstrukturen ermöglicht. In der Metallbau-Branche wird die Methode der finiten Elemente eingesetzt, um die Belastbarkeit und Stabilität von Konstruktionen zu prüfen. Beispielsweise kann die FEM-Simulation verwendet werden, um die Auswirkungen von physikalischen Belastungen auf tragende Elemente zu bewerten und so die Effizienz der Konstruktion zu steigern.
Wie unterstützt die FEM wassergekühlte Anlagensysteme?
Wassergekühlte Anlagensysteme profitieren erheblich von der FEM-Simulation, da sie eine detaillierte Analyse der thermischen und mechanischen Belastungen ermöglicht. Diese Systeme erfordern eine sorgfältige Planung und Optimierung, um maximale Effizienz und Langlebigkeit zu gewährleisten. Durch FEM können Ingenieure die thermische Ausdehnung und die daraus resultierenden Spannungen in den Elementen der Anlage simulieren, um Designentscheidungen zu treffen, die die Leistung verbessern und die Betriebskosten senken.
Wie wird eine FEM-Simulation erstellt?
Welche Schritte umfasst die Diskretisierung bei FEM?
Die Diskretisierung ist der erste Schritt bei der Erstellung einer FEM-Simulation. Dabei wird die kontinuierliche Geometrie des Bauteils in eine endliche Anzahl von Elementen unterteilt. Diese Elemente übernehmen die physikalischen Eigenschaften des Gesamtsystems und sind durch Knotenpunkte miteinander verbunden. Die Anzahl und Größe der Elemente, sowie die Dichte des Netzes, bestimmen die Genauigkeit und Rechenzeit der Simulation. Eine feine Unterteilung ermöglicht detaillierte Ergebnisse, erfordert jedoch mehr Rechenressourcen.
Wie werden Randbedingungen in der FEM definiert?
Randbedingungen sind ein wesentlicher Bestandteil der FEM-Simulation, da sie die physikalischen Grenzen und Interaktionen des Modells definieren. Sie können feste oder bewegliche Lager, Temperaturbedingungen oder aufgebrachte Lasten umfassen. Die korrekte Definition der Randbedingungen ist entscheidend, um realistische Ergebnisse zu erzielen. Sie beeinflussen direkt die Berechnung der Verformungen und Spannungen und müssen sorgfältig gewählt werden, um die physikalischen Gegebenheiten des realen Systems zu reflektieren.
Welche Solver werden in FEM-Simulationen verwendet?
Solver sind Algorithmen, die das Gleichungssystem der FEM-Simulation lösen. Es gibt verschiedene Arten von Solvern, darunter direkte und iterative Verfahren. Direkte Solver lösen das Gleichungssystem durch direkte Berechnung, während iterative Solver Näherungsverfahren verwenden, um schrittweise zur Lösung zu gelangen. Die Wahl des Solvers hängt von der Größe und Komplexität des Modells sowie von den spezifischen Anforderungen der Simulation ab. Iterative Solver sind oft effizienter bei großen, komplexen Modellen, während direkte Solver für kleinere Systeme bevorzugt werden.
Welche Herausforderungen gibt es bei der FEM-Simulation?
Wie beeinflussen Näherungsverfahren das Ergebnis?
Näherungsverfahren sind ein integraler Bestandteil der FEM, da sie die Lösung komplexer Differentialgleichungen ermöglichen. Diese Verfahren bergen jedoch das Risiko von Ungenauigkeiten, insbesondere bei unzureichend feiner Netzaufteilung oder fehlerhaften Ansatzfunktionen. Die Herausforderung besteht darin, ein Gleichgewicht zwischen Rechenaufwand und Genauigkeit zu finden, um verlässliche Ergebnisse zu erzielen, die die physikalischen Verhältnisse des Modells korrekt widerspiegeln.
Was sind die häufigsten Probleme bei der Vernetzung?
Die Vernetzung, auch als Meshing bezeichnet, ist entscheidend für die Genauigkeit der FEM-Simulation. Häufige Probleme umfassen ungenügende Netzfeinheit, inkonsistente Elementgeometrien und unzureichende Knotenverteilung. Diese Probleme können zu falschen Berechnungsergebnissen führen und die physikalische Korrektheit der Simulation beeinträchtigen. Eine sorgfältige Planung und Anpassung des Netzes sind notwendig, um diese Herausforderungen zu meistern und die Präzision der Simulation zu gewährleisten.
Wie können physikalische Verhalten korrekt abgebildet werden?
Die korrekte Abbildung physikalischer Verhalten in der FEM erfordert eine präzise Modellierung der Materialeigenschaften und Randbedingungen. Dies beinhaltet die Berücksichtigung von nicht-linearen Eigenschaften wie plastisches Verhalten oder thermische Ausdehnung. Moderne FEM-Software bietet fortschrittliche Modelle, um diese komplexen Phänomene zu berücksichtigen und realistische Simulationen zu ermöglichen. Die Herausforderung besteht darin, die richtigen Modelle und Parameter zu wählen, um die physikalische Realität so genau wie möglich nachzubilden.
Welche Vorteile bietet die FEM-Simulation für Unternehmen wie KSK GmbH?
Wie spart die FEM-Simulation Kosten im Metallbau?
Die FEM-Simulation bietet erhebliche Kosteneinsparungen im Metallbau durch die Optimierung von Designs vor der Produktion. Unternehmen wie die KSK GmbH können durch den Einsatz von FEM Entwicklungszyklen verkürzen. Dadurch werden Projektkosten gesenkt, was letztendlich zu einer höheren Wettbewerbsfähigkeit führt.
Welche Verbesserungen bringt die FEM für die Produktentwicklung?
In der Produktentwicklung ermöglicht die FEM eine detaillierte Analyse und Optimierung von Designs, bevor sie in die Produktion gehen. Diese Methode bietet tiefere Einblicke in das physikalische Verhalten von Bauteilen unter verschiedenen Lastbedingungen, was zu innovativeren und effizienteren Produkten führt. Die FEM unterstützt Ingenieure dabei, Schwachstellen frühzeitig zu identifizieren und Designänderungen vorzunehmen, die die Leistung und Zuverlässigkeit des Endprodukts erheblich verbessern.
Wie steigert FEM die Effizienz bei der Bauteilberechnung?
FEM steigert die Effizienz bei der Bauteilberechnung, indem sie schnelle und genaue Analysewerkzeuge bereitstellt. Durch die Automatisierung komplexer Berechnungen und die Möglichkeit, mehrere Varianten eines Designs schnell zu testen, können Ingenieure fundierte Entscheidungen treffen und die Entwicklungszeit erheblich verkürzen. Die FEM ermöglicht es, komplexe physikalische Phänomene zu simulieren, die mit traditionellen Berechnungsmethoden nicht einfach oder gar nicht erfassbar wären, wodurch sie einen entscheidenden Vorteil für die Optimierung von Bauteilen bietet.


Analyse und Beratung

CFD Simulation

Concept Engineering

Design Engineering
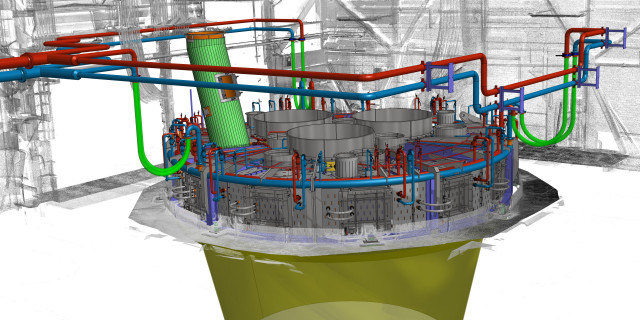
Konstruktionsbüro

Inbetriebnahme von Anlagen

Projektmanagement

Reverse Engineering
Safety Engineering

Schadensanalyse

Stahlbau-Statik
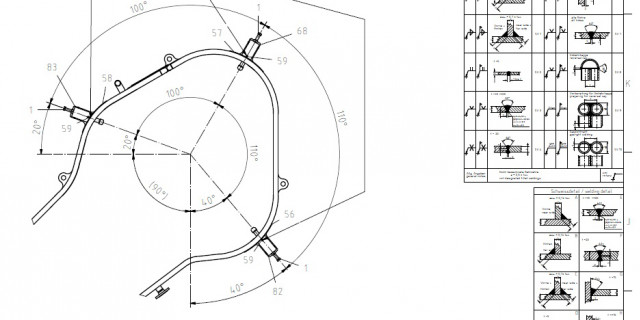
Technische Dokumentation
Inhaltsverzeichnis
- Q: Was ist die FEM-Simulation?
- Q: Wie funktioniert die Finite-Elemente-Methode?
- Q: Welche Anwendungen der FEM gibt es in der Stahlindustrie?
- Q: Welche Rolle spielt die KSK GmbH in der FEM-Simulation?
- Q: Was sind die Vorteile der Verwendung von FEM in der Metallbauindustrie?
- Q: Welche mathematischen Grundlagen liegen der FEM zugrunde?
- Q: Welche Bedeutung hat die Vernetzung bei der FEM-Berechnung?
- Q: Welche Einflüsse und Randbedingungen müssen bei der FEM berücksichtigt werden?
- Q: Wie trägt die FEM zur Entwicklung von wassergekühlten Anlagensystemen bei?
Q: Was ist die FEM-Simulation?
A: Die FEM-Simulation ist ein numerisches Verfahren zur Lösung komplexer physikalischer Problemstellungen, indem es das physikalische Verhalten eines Bauteils durch Diskretisierung in finite Elemente darstellt. Die FEM-Simulation, oder Finite-Elemente-Methode, wird häufig in der Ingenieurwissenschaft und angewandten Mathematik eingesetzt, um Spannungen, Verformungen und andere physikalische Eigenschaften von Materialien und Konstruktionen unter verschiedenen Belastungsbedingungen zu analysieren. Durch die Aufteilung eines komplexen Geometrieproblems in kleinere, einfachere Elemente kann die Methode die Gleichungen der Kontinuumsmechanik auf numerische Weise lösen.
Jedes dieser finiten Elemente ist durch Knotenpunkte verbunden, und innerhalb jedes Elements können die physikalischen Eigenschaften wie Verschiebung, Temperatur oder Druck näherungsweise beschrieben werden. Die Gesamtheit dieser einzelnen Berechnungen ergibt ein umfassendes Bild des Verhaltens des gesamten Bauteils unter spezifischen Bedingungen.
Ein wesentlicher Vorteil der FEM ist ihre Flexibilität. Sie kann auf Probleme in verschiedenen Bereichen wie Strukturmechanik, Thermodynamik und Elektromagnetismus angewendet werden. Moderne Softwarepakete ermöglichen es Ingenieuren, komplexe Simulationen durchzuführen, die sowohl lineare als auch nichtlineare Materialverhalten berücksichtigen können.
Für eine erfolgreiche FEM-Analyse sind jedoch eine sorgfältige Modellierung und die richtige Auswahl von Elementtypen und Netzfeinheit entscheidend. Eine feine Vernetzung kann zu genaueren Ergebnissen führen, erfordert jedoch mehr Rechenleistung und Zeit. Daher ist es oft ein Balanceakt zwischen Genauigkeit und Rechenaufwand.
Insgesamt bietet die FEM-Simulation eine leistungsstarke Möglichkeit, das Verhalten von Konstruktionen und Materialien vorherzusagen, was in der Entwicklung und Optimierung von Produkten und Bauwerken von unschätzbarem Wert ist.
Q: Wie funktioniert die Finite-Elemente-Methode?
A: Die Finite-Elemente-Methode funktioniert durch die Aufteilung eines Bauteils in eine Vielzahl von kleinen, einfach zu berechnenden Elementen. Diese Elemente sind durch Knotenpunkte verbunden und ermöglichen die Berechnung von Verformungen und Spannungen unter verschiedenen Lasten. Die Finite-Elemente-Methode (FEM) ermöglicht Ingenieuren und Wissenschaftlern, komplexe physikalische Probleme zu analysieren und zu lösen, indem sie große Strukturen in kleinere, überschaubare Teile zerlegen. Jedes dieser kleinen Elemente wird anhand von einfachen Gleichungen beschrieben, die seine physikalischen Eigenschaften wie Steifigkeit, Dichte und thermische Ausdehnung berücksichtigen.
Wenn eine äußere Last oder eine innere Beanspruchung auf das Bauteil wirkt, werden die Verschiebungen und Spannungen an den Knotenpunkten berechnet. Diese Informationen werden dann verwendet, um die Reaktionen der einzelnen Elemente zu bestimmen. Durch die Kombination der Ergebnisse aller Elemente kann ein umfassendes Bild der Verformungen und Spannungsverteilungen im gesamten Bauteil erstellt werden.
FEM wird in vielen Bereichen der Ingenieurwissenschaften und der angewandten Mathematik eingesetzt. Sie ist von entscheidender Bedeutung im Maschinenbau, Bauingenieurwesen, Luft- und Raumfahrttechnik sowie in der Automobilindustrie. Durch die Fähigkeit, genaue Vorhersagen über das Verhalten komplexer Strukturen unter realen Bedingungen zu liefern, trägt die Finite-Elemente-Methode dazu bei, sicherere und effizientere Designs zu entwickeln.
Die Entwicklung von leistungsfähigerer Computerhardware und spezialisierter Software hat die Anwendung der FEM erheblich erweitert, sodass noch größere und komplexere Probleme gelöst werden können. Moderne FEM-Software bietet benutzerfreundliche Schnittstellen und erweiterte Funktionen, wie z.B. nichtlineare Analysen, dynamische Simulationen und Optimierungstechniken, die es Anwendern ermöglichen, noch detailliertere und spezifischere Einblicke in ihr Design zu gewinnen.
Q: Welche Anwendungen der FEM gibt es in der Stahlindustrie?
A: In der Stahlindustrie wird die FEM zur Optimierung von Metallbau- und Schweißkonstruktionen, zur Analyse von Verformungen und zur Vorhersage der Lebensdauer von Bauteilen unter verschiedenen Belastungsbedingungen eingesetzt. Darüber hinaus spielt die Finite-Elemente-Methode (FEM) eine entscheidende Rolle bei der Verbesserung der Produktionsprozesse und der Qualität der Endprodukte. Durch die Simulation von thermischen und mechanischen Belastungen können Ingenieure potenzielle Schwachstellen in der Konstruktion frühzeitig erkennen und entsprechende Anpassungen vornehmen. Dies führt nicht nur zu einer Erhöhung der Sicherheit und Zuverlässigkeit der Produkte, sondern auch zu Kosteneinsparungen durch die Reduzierung von Materialverschwendung und Nachbearbeitungsaufwand.
Ein weiterer wichtiger Anwendungsbereich der FEM in der Stahlindustrie ist die Entwicklung neuer Legierungen und Materialien. Durch die Simulation verschiedener Szenarien können Forscher die Auswirkungen von Legierungszusätzen auf die mechanischen Eigenschaften des Stahls besser verstehen und optimieren. Dies ermöglicht die Herstellung von Materialien, die speziell auf die Anforderungen bestimmter Anwendungen abgestimmt sind, wie z.B. erhöhte Korrosionsbeständigkeit oder größere Festigkeit bei gleichzeitig geringem Gewicht.
Zusammengefasst trägt die FEM wesentlich zur Innovationskraft und Wettbewerbsfähigkeit der Stahlindustrie bei, indem sie fundierte Entscheidungen in der Produktentwicklung und Prozessoptimierung unterstützt.
Q: Welche Rolle spielt die KSK GmbH in der FEM-Simulation?
A: Die KSK GmbH, ansässig in Haltern am See, nutzt die FEM-Simulation zur Entwicklung und Optimierung von wassergekühlten Anlagensystemen, um die Effizienz und Zuverlässigkeit ihrer Produkte zu steigern. Die FEM-Simulation, oder Finite-Elemente-Methode, ermöglicht es der KSK GmbH, komplexe physikalische Prozesse präzise zu modellieren und zu analysieren. Durch die Simulation von Strömungsdynamiken und thermischen Belastungen können Ingenieure potenzielle Schwachstellen identifizieren und Designanpassungen vornehmen, bevor physische Prototypen gebaut werden. Dies führt nicht nur zu einer Verkürzung der Entwicklungszeit, sondern auch zu einer erheblichen Kostenreduktion.
Darüber hinaus erlaubt die FEM-Simulation der KSK GmbH, verschiedene Szenarien zu testen, um die Leistungsfähigkeit ihrer Systeme unter extremen Bedingungen zu gewährleisten. Dies ist besonders wichtig in Anwendungen, bei denen Zuverlässigkeit und Langlebigkeit entscheidend sind, wie etwa in der Energieerzeugung oder in industriellen Kühlprozessen.
Durch den Einsatz dieser fortschrittlichen Simulationstechniken positioniert sich die KSK GmbH als innovativer Marktführer in ihrem Bereich, der seinen Kunden hochqualitative und optimierte Lösungen bietet. Gleichzeitig trägt die Nutzung solcher Technologien zur Nachhaltigkeit bei, indem Ressourcen effizienter verwendet und der ökologische Fußabdruck der Produkte minimiert wird.
Q: Was sind die Vorteile der Verwendung von FEM in der Metallbauindustrie?
A: Die FEM ermöglicht Metallbauern, die strukturelle Integrität von Konstruktionen zu analysieren und zu optimieren, was zu sichereren und effizienteren Designs führt. Darüber hinaus trägt die Finite-Elemente-Methode (FEM) dazu bei, Materialeinsparungen zu realisieren, indem sie genauere Vorhersagen über das Verhalten von Bauteilen unter verschiedenen Lastbedingungen ermöglicht. Dies ist besonders wichtig in der heutigen Zeit, wo Nachhaltigkeit und Ressourcenschonung immer mehr an Bedeutung gewinnen. Durch die Simulation verschiedener Szenarien können Metallbauer potenzielle Schwachstellen bereits in der Entwurfsphase identifizieren und beheben, bevor physische Prototypen erstellt werden. Dies reduziert nicht nur die Kosten, sondern verkürzt auch die Entwicklungszeit erheblich.
Ein weiterer Vorteil der FEM ist die Möglichkeit, komplexe Geometrien und nichtlineare Materialienigenschaften zu berücksichtigen, die mit herkömmlichen Berechnungsmethoden nur schwer zu analysieren wären. Dies eröffnet neue Möglichkeiten im Design und ermöglicht innovativere und individuellere Lösungen. Die Integration von FEM in den Arbeitsprozess erfordert jedoch auch eine entsprechende Schulung und Erfahrung, um die Ergebnisse korrekt interpretieren und umsetzen zu können. Insgesamt stellt die FEM ein unverzichtbares Werkzeug im modernen Metallbau dar, das die Qualität, Sicherheit und Effizienz von Bauprojekten maßgeblich verbessert.
Q: Welche mathematischen Grundlagen liegen der FEM zugrunde?
A: Die mathematischen Grundlagen der FEM beinhalten die Lösung von Differentialgleichungen durch Numerische Verfahren wie das Näherungsverfahren und die Methode der gewichteten Residuen. Die mathematischen Grundlagen der Finite-Elemente-Methode (FEM) beinhalten die Lösung von Differentialgleichungen durch numerische Verfahren wie das Näherungsverfahren und die Methode der gewichteten Residuen. Diese Ansätze ermöglichen es, komplexe physikalische Probleme zu modellieren und zu analysieren, die analytisch schwer lösbar sind. Die FEM zerlegt ein Kontinuum in eine endliche Anzahl von Elementen, wobei die Lösung innerhalb jedes Elements durch spezielle Ansatzfunktionen, oft Polynomfunktionen, angenähert wird.
Ein wesentlicher Schritt in der FEM ist die Diskretisierung des Problembereichs, was bedeutet, dass das kontinuierliche Problem in ein endlich-dimensionales Problem überführt wird. Dies wird erreicht, indem der Problembereich in kleinere, überschaubare Teile unterteilt wird, die sogenannten Finite Elemente, und die Differentialgleichungen auf diese Elemente angewendet werden. Die Knotenpunkte, an denen die Elemente zusammentreffen, sind entscheidend für die Definition der Problemlösung.
Die Methode der gewichteten Residuen, zu der die Galerkin-Methode gehört, wird häufig verwendet, um die Näherungslösungen zu optimieren. In diesem Rahmen wird das Residuum, der Unterschied zwischen der exakten und der approximierten Lösung, gewichtet und minimiert.
Ein weiterer wichtiger Aspekt der FEM ist die Formulierung der Elementsteifigkeitsmatrix und der globalen Steifigkeitsmatrix des Systems. Diese Matrizen bilden die Grundlage für die Lösung der resultierenden algebraischen Gleichungssysteme, die durch die Diskretisierung entstehen. Für die effiziente Berechnung dieser Matrizen werden verschiedene numerische Integrationstechniken eingesetzt.
In der Praxis wird die FEM in einer Vielzahl von Ingenieuranwendungen eingesetzt, darunter Strukturmechanik, Thermodynamik, Elektromagnetismus und Fluiddynamik. Die Methode ist besonders wertvoll in der Luft- und Raumfahrtindustrie, im Bauwesen, in der Automobilindustrie und in der Biomechanik, wo sie zur Simulation und Optimierung von Bauteilen und Systemen verwendet wird.
Q: Welche Bedeutung hat die Vernetzung bei der FEM-Berechnung?
A: Die Vernetzung ist entscheidend, da sie die Geometrie des Bauteils in Elemente unterteilt. Die Feinheit der Unterteilung und die Dichte des Netzes beeinflussen die Genauigkeit der FEM-Berechnung. Die Vernetzung ist entscheidend, da sie die Geometrie des Bauteils in Elemente unterteilt. Die Feinheit der Unterteilung und die Dichte des Netzes beeinflussen die Genauigkeit der FEM-Berechnung. Eine feinere Netzstruktur kann zu präziseren Ergebnissen führen, da sie in der Lage ist, komplexere Geometrien und Belastungskonzentrationen detaillierter abzubilden. Allerdings erhöht eine höhere Netzfeinheit auch die Berechnungszeit und den Rechenaufwand erheblich.
Ein ausgewogenes Verhältnis zwischen Netzfeinheit und Rechenaufwand ist daher entscheidend für eine effiziente und genaue Analyse. In der Praxis wird oft eine Verfeinerungsmethode angewendet, bei der das Netz in kritischen Bereichen des Bauteils, wie zum Beispiel an den Stellen mit hohen Spannungskonzentrationen oder komplexen Geometrien, feiner gestaltet wird. In weniger kritischen Bereichen kann das Netz gröber gehalten werden, um Ressourcen zu sparen.
Zusätzlich zur Netzfeinheit spielt auch die Art der verwendeten Elemente eine Rolle. Unterschiedliche Elementtypen, wie z.B. lineare oder quadratische Elemente, können je nach Anwendungsfall unterschiedliche Vor- und Nachteile haben. Quadratische Elemente bieten in der Regel höhere Genauigkeit bei der Darstellung von Krümmungen und komplexen Formen, während lineare Elemente einfacher und schneller zu berechnen sind.
Die Wahl der richtigen Vernetzung und der geeigneten Elementtypen ist somit ein entscheidender Schritt im FEM-Prozess, der sowohl fundiertes technisches Wissen als auch Erfahrung erfordert. Ingenieure und Analytiker müssen sorgfältig abwägen, um eine optimale Balance zwischen Genauigkeit und Effizienz zu erreichen, was letztendlich zu zuverlässigeren und wirtschaftlicheren Designlösungen führt.
Q: Welche Einflüsse und Randbedingungen müssen bei der FEM berücksichtigt werden?
A: Bei der FEM müssen physikalische Einflüsse wie Lasten, Materialeigenschaften und Randbedingungen, die das physikalische Verhalten des Bauteils beeinflussen, berücksichtigt werden. Bei der Finite-Elemente-Methode (FEM) ist es entscheidend, eine genaue Modellierung der physikalischen Einflüsse sicherzustellen, um valide und zuverlässige Ergebnisse zu erhalten. Lasten können statisch oder dynamisch sein und müssen entsprechend ihrer Natur und Wirkung auf das Bauteil präzise definiert werden. Materialeigenschaften wie Elastizitätsmodul, Poisson'sche Zahl, Dichte und Festigkeit sind ebenfalls von zentraler Bedeutung, da sie die Reaktion des Materials auf die einwirkenden Kräfte bestimmen.
Randbedingungen spielen eine wesentliche Rolle, da sie die Bewegung des Bauteils einschränken oder bestimmten Bewegungen erlauben. Diese können als feste Einspannungen, freie Lagerungen oder als symmetrische Bedingungen formuliert sein. Eine sorgfältige Definition der Randbedingungen ist notwendig, um realistische Simulationen zu gewährleisten.
Des Weiteren müssen bei der FEM-Netzerstellung die Geometrie des Bauteils und die Detaillierungsgrade der Netzstruktur berücksichtigt werden. Eine feiner aufgelöste Netzstruktur kann genauere Ergebnisse liefern, erfordert jedoch mehr Rechenleistung und Zeit. Daher ist es wichtig, ein Gleichgewicht zwischen Genauigkeit und Effizienz zu finden.
Nach der Modellierung und Simulation sind Ergebnisinterpretation und Validierung entscheidende Schritte, um die Richtigkeit der Simulation zu überprüfen. Hierbei können Vergleichsstudien mit experimentellen Daten oder analytischen Lösungen helfen, die Qualität und Zuverlässigkeit der FEM-Ergebnisse sicherzustellen.
Q: Wie trägt die FEM zur Entwicklung von wassergekühlten Anlagensystemen bei?
A: Die FEM hilft bei der Entwicklung von wassergekühlten Anlagensystemen, indem sie die thermischen und mechanischen Belastungen simuliert und optimiert, um die Effizienz und Langlebigkeit der Systeme zu verbessern. Die Finite-Elemente-Methode (FEM) ermöglicht es Ingenieuren, detaillierte Modelle von wassergekühlten Anlagensystemen zu erstellen, die sowohl die Materialien als auch die spezifischen Betriebsbedingungen berücksichtigen. Durch die Simulation verschiedener Szenarien können kritische Bereiche identifiziert werden, in denen thermische Spannungen oder mechanische Belastungen zu potenziellen Ausfällen führen könnten.
Ein weiterer Vorteil der FEM ist die Möglichkeit, verschiedene Designoptionen schnell zu evaluieren. Dies spart nicht nur Zeit und Kosten, sondern erlaubt auch eine präzisere Optimierung der Systeme. Beispielsweise können Ingenieure mithilfe von FEM-Analysen feststellen, wie Änderungen in der Geometrie oder Materialauswahl die Wärmeableitung und strukturelle Integrität beeinflussen.
Darüber hinaus unterstützt die FEM dabei, die Kühlleistung zu maximieren und gleichzeitig den Energieverbrauch zu minimieren. Durch die Identifizierung der effizientesten Kühlstrategien kann die FEM dazu beitragen, die Gesamtbetriebskosten der Anlagensysteme zu senken.
In der Praxis führt der Einsatz der FEM zu robusteren und zuverlässigeren wassergekühlten Anlagensystemen, die unter extremen Bedingungen betrieben werden können, ohne die Gefahr von Ausfällen oder ineffizienten Betriebszuständen. Dies ist besonders wichtig in Industrien wie der Energie- oder Stahlerzeugung, wo der reibungslose Betrieb von Anlagen entscheidend für den Erfolg ist.
